
The algorithm is exactly the same as for the oneĭimensional case, only the math is a bit more tricky.
Savitsky-Golay filters can also be used to smooth two dimensional dataĪffected by noise. Two dimensional data smoothing and least-square gradient estimate ¶ concatenate (( firstvals, y, lastvals )) return np. A * rate ** deriv * factorial ( deriv ) # pad the signal at the extremes with # values taken from the signal itself firstvals = y - np. mat ( for k in range ( - half_window, half_window + 1 )]) m = np.
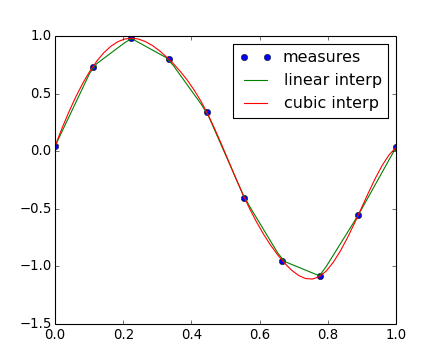
int ( order )) except ValueError, msg : raise ValueError ( "window_size and order have to be of type int" ) if window_size % 2 != 1 or window_size < 1 : raise TypeError ( "window_size size must be a positive odd number" ) if window_size < order + 2 : raise TypeError ( "window_size is too small for the polynomials order" ) order_range = range ( order + 1 ) half_window = ( window_size - 1 ) // 2 # precompute coefficients b = np. Flannery Cambridge University Press ISBN-13: 9780521880688 """ import numpy as np from math import factorial try : window_size = np. Numerical Recipes 3rd Edition: The Art of Scientific Computing W.H. Golay, Smoothing and Differentiation of Data by Simplified Least Squares Procedures. Examples - t = np.linspace(-4, 4, 500) y = np.exp( -t**2 ) + np.random.normal(0, 0.05, t.shape) ysg = savitzky_golay(y, window_size=31, order=4) import matplotlib.pyplot as plt plt.plot(t, y, label='Noisy signal') plt.plot(t, np.exp(-t**2), 'k', lw=1.5, label='Original signal') plt.plot(t, ysg, 'r', label='Filtered signal') plt.legend() plt.show() References. The main idea behind this approach is to make for each point a least-square fit with a polynomial of high order over a odd-sized window centered at the point. Notes - The Savitzky-Golay is a type of low-pass filter, particularly suited for smoothing noisy data. deriv: int the order of the derivative to compute (default = 0 means only smoothing) Returns - ys : ndarray, shape (N) the smoothed signal (or it's n-th derivative).

order : int the order of the polynomial used in the filtering. window_size : int the length of the window. Parameters - y : array_like, shape (N,) the values of the time history of the signal. It has the advantage of preserving the original shape and features of the signal better than other types of filtering approaches, such as moving averages techniques. The Savitzky-Golay filter removes high frequency noise from data. #!python def savitzky_golay ( y, window_size, order, deriv = 0, rate = 1 ): r """Smooth (and optionally differentiate) data with a Savitzky-Golay filter.


 0 kommentar(er)
0 kommentar(er)
